In today’s post, we will discuss another OSPF filtering technique: Filtering with Administrative Distance.

Before start digging into how to apply this type of filtering let’s recall how Cisco routers pick the best path:

Prefix length:

Routers always use this method first; it compares the destination network with the available prefixes in the routing table before forward packets.  Longest prefixes are always preferred.  In case, there is more than one possible route with the same prefix-length then the router picks the one with lower Administrative Distance.

Administrative Distance:

The administrative distance (AD) is the given level of “trust” of the route source.  If the router learns a route from more than one routing protocol, then the AD is compared between them.  The prefix with lower administrative distance is preferred.  In case, there is more than one possible route with the same prefix-length and the same administrative distance, then the router picks the one with lowest Metric.   If the administrative distance is 255, then the router simply don’t trust the route, therefore, is not installed in the routing table.     Here you can find more information about AD.

Metric:

The metric is the calculated value for a given prefix to reach a destination.  Each routing protocol uses different ways to calculate their metric.   In a case where prefix-length, administrative distance, and metric are the same, then routers end up doing load balancing.

OSPF uses three different administrative distances: intra-area, inter-area and external routes.  However, the default value for all of them is 110.   In a future post, we will discuss how modifying each one for traffic-engineering purposes.    In today’s post, we will focus in filtering using the distance command.

For filtering purposes, the administrative distance can be modified in per-prefix or per-neighbor basis in OSPF.

There is some confusion about how this command must be used in OSPF for filtering purposes, in the documentation the command is listed as follows:

distance weight ip-address wildcard-mask {access-list name}

The confusion lies in the ip-address/wildcard-mask in the command.  Therefore, let me clarify the command with my own definition of the parameters:

distance 255 {Neighbor-RID 0.0.0.0} {access-list} OSPF process command.

Ok, when filtering in OSPF the weight must be set to 255, this will make the desired prefix or set of prefixes untrustworthy.  Therefore, the prefix or prefixes won’t be installed in the routing table.  Also, note I have changed the ip-address and wildcard mask for {neighbor-RID 0.0.0.0}, here is where the confusion lies.   It is believed that the prefix to be filtered is entered here; however is the Router-ID of the neighbor advertising the prefix but it is defined as if it were a host in an access-list (I don’t know why this hasn’t been changed yet.).  Finally, the access-list is used to define the prefix or set of prefixes to be filtered.

Let’s use the same topology used in the previous post for the examples:

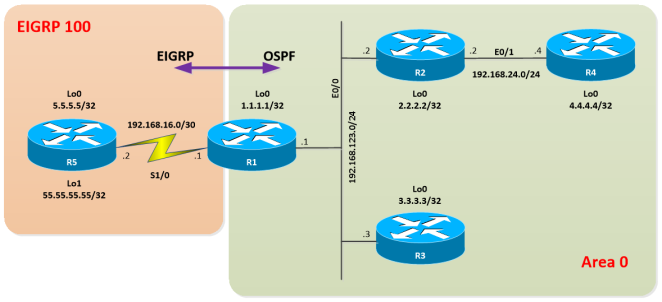
Here you can download the diagram and configuration files: OSPF-Filtering – Part III

Ok, let’s do some filtering.

Goal 1:

Configure OSPF filtering on R3, in such way the ip address 4.4.4.4/32 does not show in its routing table.  Do not use distribute-lists for this goal.

Let’s start by taking a look to the route to be filtered from R3’s perspective:

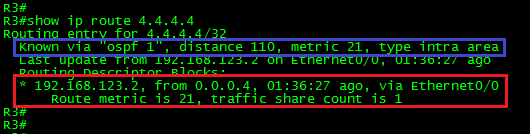
As seen in the above output, the route 4.4.4.4/32 is an OSPF intra-area route and it is being advertised with the default OSPF distance (110) and a metric of 21.   The next-hop to reach the route is 192.168.123.2, from 0.0.0.4 which is the Router-ID of R4 via the interface Ethernet0/0.

At the moment, we have all the required ingredients to create the filter, so let’s do it.

In R3:

!
access-list 34 permit 4.4.4.4
!
router ospf 1
distance 255 0.0.0.4 0.0.0.0 34
exit
!

Now, let’s take a look at the routing table in R3:

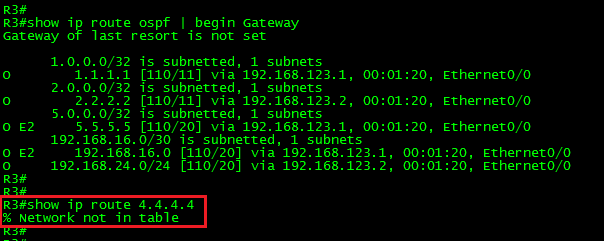
As can be seen, the route is no longer in the Global RIB.

Now, let’s see what OSPF have to say about the route:

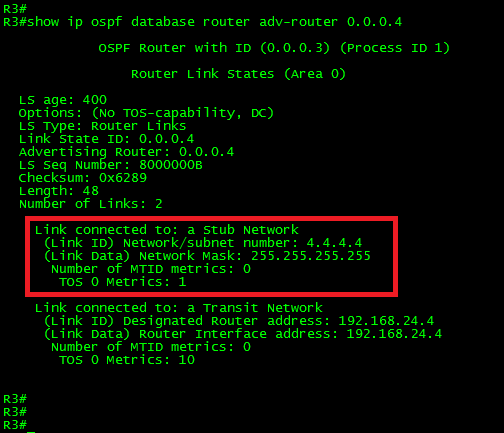
The Type-1 LSA is still present in the link-state database (LSDB).   What about the OSPF RIB?

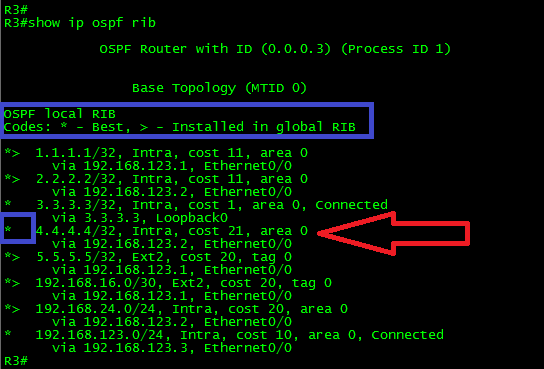
As shown above, the route is present in the OSPF RIB but without the “greater than” sign.  This means the route wasn’t installed in the Global RIB.

Worth mentioning that modifying the administrative distance affects only the routing table.  It does not change the OSPF LSDB.   Therefore, it may cause a traffic black hole, a routing loop or another undesired behavior.   Use it carefully.

It is time to close this post.  In the next one, we will discuss OSPF LSA Database Filtering.

Thank you for visiting.